안녕하세요? 친절한 수학쌤입니다.
지난 글에서 일차방정식의 뜻과 풀이에 대해서 설명했는데요~~
오늘은 일차방정식 중에서 복잡한 일차방정식의 풀이에 대해서 설명하도록 하겠습니다.
괄호( ) 가 있는 식, 계수가 소수인 경우, 계수가 분수인 경우 이 세가지에 대해서 이야기 해 볼려고 합니다.

먼저 괄호( ) 가 있는 식의 경우는 분배법칙을 이용하여 식을 정리한 후 풀이를 합니다.
예를 들어 볼께요~
(1) -2(x-5) = -8+x (2) -(x-2) = 3(x+6)
-2x+10 = -8+x -x+2 = 3x+18
-2x-x = -8-10 -x-3x = 18-2
-3x = -18 -4x = 16
x = 6 x = -4
다음으로 계수가 소수인 경우에는 식의 양변에 10이나 100이나 1000 ... 중에서 적당한 수를 곱해서
계수를 정수로 고쳐서 풀이합니다.
(1) 0.3x-1 = 0.1x+0.4 (2) 0.06x+0.2 = 0.02x-0.12
3x-10 = x+4 6x+20 = 2x-12
3x-x = 4+10 6x-2x = -12-20
2x = 14 4x = -32
x = 7 x = -8
마지막으로 계수가 분수인 경우에는 식의 양변에 분모의 최소공배수를 곱해서
계수를 정수로 고쳐서 풀이합니다.
(1) 다음 식은 세 분수의 분모 (2, 5, 10) 의 최소공배수가 10이기 때문에 양변에 10을 곱해서 계수를
정수로 바꿀수 있는데 여기서 중요한 것은 모든 항에 10을 곱해야 한다는 것입니다.
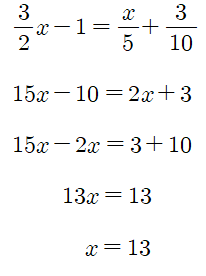
(2) 다음 식은 분수 형태 중에서 한 분모에 분자는 두개의 항으로 되어 있어서 이런 경우에 주의할 점은
최소공배수를 곱하되 분자를 괄호를 써서 분배하면 계산에 실수가 없습니다.


마지막 덤으로 좀더 복잡하게 괄호, 소수, 분수 세 경우가 섞여 있을 때 어떻게 풀이하는지, 주의점은 어떤것이 있는지 예를 들어 볼께요.
(1) 다음의 경우 소수와 괄호가 섞여 있는 경우인데 우선 양변에 10을 곱해서 계수를 정수로 바꿔야 하는데 여기서 중요한 것은 괄호 안이나 밖 중에서 한 군데만 10을 곱해야 합니다.

(1) 소수와 분수와 괄호가 썪여 있는 경우는 소수를 분수로 고친 다음에 양변에 분모의 최소공배수를
곱하면 됩니다.

여러 문제들을 풀어보면서 연습하시기 바랍니다.
다음에는 일차방정식의 활용 문제들 풀어볼께요~
모두 화이팅!!!

'수학' 카테고리의 다른 글
| [중1수학]속력에 관한 일차방정식의 활용 (0) | 2024.06.28 |
|---|---|
| [중1수학]일차방정식의 활용 - 연속하는 수, 자리의 숫자, 나이, 과부족, 일에관한 문제 (0) | 2024.06.28 |
| [중1수학]일차방정식의 뜻과 풀이 (0) | 2024.06.21 |
| [중1수학] 문자와 식 - 일차식의 계산 (1) | 2024.03.09 |
| [중1 수학] 문자와 식(항, 계수, 차수, 동류항, 다항식, 단항식)-새로운 용어 뽀개기 (0) | 2024.03.08 |