안녕하세요? 친절한 수학쌤입니다.
오늘은 일차방정식에서 빼놓을 수 없는 거. 속. 시 문제에 대해서 알아보겠습니다.
우선 거리와 속력과 시간의 관계에 대해서 알아야 하는데요~
간단하게 무당벌레 그림으로 공식을 설명하는 경우가 많죠^^

위 그림에서 나올 수 있는 공식은 세가지 인데요~

거.속.시 문제를 풀 때 가장 많이 사용되는 공식은 두번째에 있는 공식이므로 반드시 외워 두세요!!!
그러면 거리, 속력, 시간에 관한 문제를 유형별로 알아보도록 하겠습니다.

1. 속력이 바뀌는 경우
문제) 거리가 x ㎞ 인 두 지점 사이를 갈 때는 시속 3㎞, 올 때는 시속 2㎞ 로 왕복하였더니 1시간이
걸렸습니다. 거리를 구하시오.
풀이) 1단계 : 거리를 x라 두면
2단계 : 방정식을 세우면

3단계 : 방정식을 풀면

4단계 : 두 지점사이의 거리는


2. 시간 차가 생기는 경우
문제) 성수가 산악 자전거를 타고 산 정상까지 올라갔다 내려오는데 올라갈 때는 시속 4㎞, 내려올 때는
같은 길을 시속 12㎞ 의 속력으로 달렸더니 올라갈 때보다 내려올 때 50분 적게 걸렸습니다. 이때
성수가 올라간 거리를 구하시오.
풀이) 문제를 풀기 전에 주의할 점은 속력이 시속으로 나와 있기 때문에 시간도 50분을 시간으로
바꿔서 풀어야 한다는 점입니다.
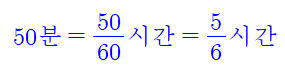
1단계 : 성수가 올라간 거리를 x라 두면
2단계 : 방정식을 세우면

3단계 : 방정식을 풀면

4단계 : 성수가 올라간 거리는 5㎞ 이다.

3. 시간 차를 두고 출발하는 경우
문제1) 동생이 집을 출발한 지 12분 후에 형이 자전거를 타고 동생을 따라 나섰다. 동생은 분속 60m로
걷고, 형은 분속 150m로 자전거를 타고 따라 간다면 형이 출발한지 몇 분 후에 동생을 만날 수
있는지 구하시오.
풀이) 1단계 : 형이 출발한 후 동생을 만날 때까지 걸린 시간을 x라 두면
2단계 : 방정식을 세우면 60(x+12)=150x
3단계 : 방정식을 풀면 60x+720=150x
60x-150x=-720
-90x=-720
x=8
4단계 : 형은 출발한지 8분만에 동생을 만날 수 있다.
문제2) 둘레의 길이가 4㎞ 인 호수의 둘레를 동욱이와 민성이가 걷고 있다. 동욱이는 1분에 120m 의
속력으로, 민성이는 1분에 80m 의 속력으로 같은 방향으로 동시에 출발하였다. 두 사람은 출발
한지 몇 분 후에 처음으로 다시 만나게 되는지 구하시오.
풀이) 문제를 풀기 전에 주의할 점은 속력이 분속으로 나와 있기 때문에 호수의 둘레의 길이도
4000m 로 바꿔서 풀어야 한다는 점입니다.
1단계 : 두 사람이 다시 만나는데 걸리는 시간을 x라 두면
2단계 : 방정식을 세우면 120x-80x=4000
3단계 : 방정식을 풀면 120x-80x=4000
40x=4000
x=100
4단계 : 두 사람은 100분 후에 다시 만나게 된다.

4. 마주보고 출발하는 경우
문제) 둘레의 길이가 12㎞ 인 호수 공원이 있다. 오전 9시 지훈이와 연우는 같은 지점에 서 있고 연우는
시속 3㎞ 의 속력으로, 지훈이는 반대 방향으로 시속 5㎞ 의 속력으로 걷기 시작했다. 두 사람이
다시 만나는 시각을 구하시오.
풀이) 1단계 : 두 사람이 다시 만나는데 걸리는 시간을 x라 두면
2단계 : 방정식을 세우면 3x+5x=12
3단계 : 방정식을 풀면 3x+5x=12
8x=12
x=1.5
4단계 : 두 사람은 1시간 30분 후에 다시 만나게 된다. 따라서 10시 30분에 다시 만나게 된다.

'수학' 카테고리의 다른 글
| [중1수학]기본도형-점, 선, 면, 각 (0) | 2024.08.28 |
|---|---|
| [중1수학]농도에 관한 일차방정식의 활용 (0) | 2024.08.16 |
| [중1수학]일차방정식의 활용 - 연속하는 수, 자리의 숫자, 나이, 과부족, 일에관한 문제 (0) | 2024.06.28 |
| [중1수학]복잡한 일차방정식의 풀이 (0) | 2024.06.26 |
| [중1수학]일차방정식의 뜻과 풀이 (0) | 2024.06.21 |